

In this study, the sensitivity analysis of bed changes due to the various sediment transport equations have been conducted for 80km reach of the Lower Nakdong River using the HEC-6 which is one dimensional numerical model. The bed elevation changes according to the different sediment transport formulas were compared and analyzed quantitatively. As a result of the numerical simulation, the final bed elevation calculated by Engelund and Hansen (1967), Ackers and White (1973), and Yang (1979) formulas was similar to one another in configuration. The bed change simulated by Engelund and Hansen (1967) were greatest among them, for example, 5.5m deposition and 2.9m erosion for 100 years. Also, in the case of Toffaleti (1969) equation, the maximum bed deposition of 8.04m after 100 years was induced at the 73km location upstream of the Nakdong River Estuary Barrage. Meyer-Peter-Müller (1948) and Wilcock (2001) formulas produced the deposition only at the upstream end and there was little bed change in the downstream area. The unreal bed configuration of continuously up and down pattern was simulated by Laursen (1958) transport equation.
정원준 대리, 도시개발부(wjjeong@samaneng.com)
위용민 부장, 도시개발부(ymwe@samaneng.com)
마길동 차장, 도시개발부(kdma@samaneng.com)
1. 서 론
하상 변동에 관한 수치모의 연구는 하천유역내의 수리구조물의 설계 및 유지관리, 하도의 안정화, 홍수터 관리, 저수지의 설계 및 운영 등 수자원 개발 및 관리를 위한 하천계획에 필요한 기본적 요소 중 하나이다. 하지만 현재 우리나라의 하상변동에 대한 연구는 단일 유사량 공식을 민감도 분석 없이 그대로 적용하여 추정하고 있으며 이는 하천마다 각기 다른 하천특성을 고려하지 않고 유사량 공식을 적용한 것으로 정확한 하상변동 예측을 기대할 수 없다. 이러한 유사량 공식 적용에 의한 하상변동 예측결과가 하천 계획 및 관리에 직접 이용할 수 있을 정도의 수준에 도달하기 위해서는 다양한 유사량 공식의 적용을 통한 하상변동 민감도 분석이 반드시 필요하다.
기존 하상변동에 대한 연구는 Thomas와 Prasuhn (1977)이 에너지방정식을 시산법으로 푸는 HEC-6 모형을 제안한 이후부터 본격적으로 이루어지기 시작하였다. Chen 등(1975)은 St. Venant 방정식을 이용하여 부정류 해석이 가능한 UUWSR 모형을 개발하였고 Chang과 Hill (1977)은 샌디에고대학에서 1972년부터 수행된 연구를 바탕으로 FLUVIAL-11 모형을 개발하였다. 그 후 Yang (1986, 1998)은 이를 발전시켜 BRALLUVIAL과 GSTARS 모형을 개발하여 모형의 적용성을 검토하였다. 국내의 하상변동에 대한 수치모의 연구는 남선우(1978)가 Brown 공식을 이용하여 팔당댐에서 행주대교 구간의 하상변동을 예측한 것이 시초라 할 수 있다. 그 후, 박정웅(1984)이 St. Venant 방정식을 차분화하여 한강 하류부에 적용시켰으며 Toffaleti (1969) 공식을 이용하여 하상토 입경변화를 고려하였다. 우효섭과 유권규(1991)는 하상변동 예측모형의 비교, 분석을 통하여 하상변동에 관한 이론을 정리하고 HEC-6 모형을 비롯한 기존의 하상변동모형들을 비교, 분석하였으며 HEC-6 모형을 충주댐 하류구간과 대청댐 하류구간에 적용시켜 이론적 및 실무적으로 한층 더 발전시켰다. 그 후 비교적 활발한 연구가 진행되어 서일원(1994)은 GSTARS 모형을 금강 대청댐 하류구간과 한강팔당댐 하류구간에 적용시켰고 고수현(2004) 등은 HEC-6 모형을 이용하여 태화강에 방사보 유무와 세 가지 유량빈도에 따른 유사량 공식별 하상변동량을 산정하는 연구를 수행하여 유사량 공식에 따라 유사량의 차이가 크게 나타낸다는 것을 밝혔다. 이와 같이 하상변동에 대한 다양한 연구가 있었지만 대부분 새로운 모형의 개발과, 기존 모형들 간의 비교 및 검증, 단일 유사량 공식 적용, 홍수 시 단기 모의만을 가지고 진행 된 연구가 대부분이고 다양한 유사량 공식을 이용하여 실제유역에 적용함으로서 유사량 공식에 대한 결과를 비교, 분석한 연구는 매우 드물다. 본 연구에서는 대상하천인 낙동강 하류 80km 구간에서 다양한 유사량 공식이 적용 가능한 HEC-6 모형을 선정하여 동일한 수리조건에 모의기간 1년, 10년, 100년의 장기하상변동모의를 실시하였고 그 결과를 비교하여 유사량 공식에 따른 하상변동의 민감도 분석을 하였다.
2. HEC-6 모형 및 유사량 공식
본 연구에서 적용된 HEC-6 모형은 미공병단 수문연구센터에서 개발한 하천과 저수지에서 세굴과 퇴적계산을 위한 수치모의 모형으로 HEC-RAS 4.0에서 통합된 모형이다. 연속 수문자료는 여러 가지 유량과 지속 기간을 지닌 일련의 준정상류 흐름으로 나누어 적용하며 각 횡단면별로 에너지 경사, 유속, 수심 등을 계산한다. 이에 따라 각각의 흐름에 대한 수면 곡선을 결정해 단면별로 유사 이송 잠재능을 계산한다. 이 운송능과 흐름사상의 지속 시간을 이용하여 각 구간별로 유사의 부피를 계산하고 각 횡단면별로 세굴과 퇴적량을 계산하여, 이에 따라 횡단면의 형태를 조절한다. 그 다음에는 주어진 일련의 수문 사상의 다음 흐름 사상에 대하여, 앞의 계산에서 수정된 하천 단면을 가지고 위의 과정을 반복한다. HEC-6 모형의 특징은 다지하천에서의 유사이송 모의가능, 이동상・고정상을 구분하여 적용 가능, 유량에 따른 하천 폭의 결정으로 유사퇴적 및 세굴의 측정방법의 자동결정, 선택폭이 넓은 다양한 유사량 공식의 적용 등을 들 수 있다.
HEC-6 모형에서 적용가능한 유사이송 공식은 총 7가지로 분류할 수 있다(Table 1). 우선 소류력을 기본개념으로 한 Ackers and White (1973) 공식, Engelund and Hansen (1967) 공식, Yang (1979) 공식은 기존 연구 동향을 보면 다른 공식들에 비하여 비교적 정확한 모의결과를 나타낸다(김진흥 등, 2002, 우효섭 등, 1991). 입자크기에 따라 구분 되는 유사이송 공식은 Meyer-Peter-Müller (1948) 공식, Laursen (1958) 공식, Wilcock (2001) 공식이 있다. Meyer-Peter-Müller (1948) 공식과 Wilcock (2001) 공식은 입자크기가 보통 5mm이상일 경우 모의에 적합한 공식이며 Laursen (1958) 공식은 비교적 가는 모래 또는 굵은 실트로 구성된 실험실 수로와 수심이 얕은 하천의 경우 모의에 적합한 공식이다. 전단응력을 기본개념으로 한 Toffaleti (1969) 공식은 대하천에서 모의에 적합한 공식이다(Yang, 2003).
Table 1. Applicable sediment transport formulas in the HEC-6 model

3. 적용대상 하천 및 입력자료
3.1 낙동강 하류
본 연구의 대상유역인 낙동강은 한반도 남동부에 위치하여 북쪽으로 한강유역, 서쪽으로는 금강 및 섬진강 유역과 접하고, 동쪽으로는 태백산맥이 동해안 유역과 분수령을 형성하는 우리나라 제2의 하천유역으로서 유역 면적은 대략 23,384km2이며 유로는 510km로 국내 최장 하천이다(건설교통부, 2006). 낙동강 본류는 동쪽의 태백산맥과 서북쪽의 속리산, 덕유산, 지리산으로 이어지는 소백산맥으로 둘러싸인 낙동강유역의 중심부를 관류하고 있으며, 유로는 산악으로 인하여 최단거리로 유하하지 못하고 유향을 네 차례나 급변하면서 우회하여 남해안으로 유입된다. 낙동강 하류의 하상경사는 0.0001에서 0.0002 사이로 매우 완만하다. 이러한 완만한 경사로 인해 염수침입이 발생하여 이를 막기 위해 1983년부터 1987년에 걸쳐 하구둑이 건설되었다. 낙동강 하구둑의 건설은 염수침입의 방지라는 긍정적인 효과 외에 하구둑으로 인한 유속 감소로 인해 상류에 유사가 퇴적되는 문제점도 있다. 따라서 홍수시 상류 수로의 통수능 확보를 위해 연간 619,500m3에 해당되는 퇴사를 커터를 이용한 펌프 준설공법을 이용, 준설하고 있는 실정이다(한국수자원공사, 2007). 낙동강은 연중 강우량의 50%에 해당되는 강우량이 6월부터 9월 사이에 집중되어 있으며 이러한 강우량 편중 현상으로 인해 최대 유량과 최소 유량의 비를 나타내는 하상계수가 다른 하천에 비해 10배에서 많게는 100배 더 큰 것으로 나타났다.

Fig 1. Study area of the Lower Nakdong River
3.2 HEC-6 모형 입력자료
HEC-6 모형의 입력자료로는 지형, 하상토, 유사량, 유량, 수위자료 등이 있다. 본 연구에서는 낙동강 하천정비기본계획(건설교통부, 1991)의 지형자료를 이용하였으며 진동지점에서 낙동강하구둑까지 총 80km를 모의 대상구간으로 선정하였다(Fig 1). 하상토 자료와 유사량 자료는 낙동강 하구둑 유지관리 개선방안 연구 보고서(한국수자원공사, 2008)의 자료를 활용하였다. 2002년도 진동지점의 일 유량과 2002년도 낙동강하구둑 수위(Fig 2)를 상류 및 하류단의 경계조건으로 1년, 10년, 100년의 기간에 대해 장기하상변동 모의를 실시하였고 조도계수는 0.025(서낙동강 하천정비기본계획, 2001), 하상토의 중앙입경은 진동지점 0.3mm, 구포지점 0.25mm(한국수자원공사, 2008), 수온은 낙동강의 1년 평균수온인 12.9°C를 적용하였다. 7가지의 유사량 공식을 각각의 모의 기간에(1년, 10년, 100년) 적용, 총 21 조건의 모의를 수행하였다.

Fig 2. Flow discharge and elevation data at the Lower Nakdong River in 2002
4. 모의 결과 및 분석
본 연구에서는 HEC-6 모형을 이용하여 낙동강 진동지점에서 하구둑까지 80km 구간에 대해 유사량 공식별 하상변동 모의를 수행하였다. 모의 결과는 Fig 3에서 9와 같고 유사량 공식별 최대 퇴적 및 침식 정도를 Table 2에서 4와 같이 정리하였다.
Fig 3에서 5의 결과를 보면 Ackers and White (1973) 공식, Yang (1979) 공식, Engelund and Hansen (1967) 공식은 소류력이라는 동일한 기본개념으로 만들어진 공식으로 하상변동의 전체적 양상이 비슷하게 나타났다. 다만 여기서 주목해야 할 점은 Engelund and Hansen (1967) 공식이 세 공식들 중 가장 많은 하상변동을 모의하였고 그 뒤로 Ackers and White (1973) 공식, Yang (1979) 공식의 순으로 하상변동이 큰 것으로 나타났다. Table 4를 보면 Ackers and White (1973) 공식, Yang (1979) 공식, Engelund and Hansen (1967) 공식은 하류에서 52km 부분의 지점에서 100년 후 4.92m, 4.48m, 5.48m의 퇴적이 발생한 것을 알 수 있다. 전체적인 하상변동의 양상과 정량적인 수치로 판단했을 경우에도 Engelund and Hansen (1967) 공식이 가장 큰 하상변동을 예측하는 것으로 나타났다.
Meyer-Peter-Müller (1948) 공식과 Wilcock (2001) 공식의 경우 하상토의 중앙입경이 큰 자갈하천에서 적용 가능한 소류사 공식으로 1년 모의와 10년 모의에선 하상변동이 거의 나타나지 않았으며 100년 모의의 경우, 하류구간에서 중류구간 사이에는 퇴적이 심하게 발생하지 않은 것에 비해 상류 82km 지점에서 Meyer-Peter-Müller (1948) 공식은 3.11m, 상류 84km 지점에서 Wilcock (2001) 공식은 5.62m로 최대퇴적이 나타나는 것을 알 수 있다. Laursen (1958) 공식은 Meyer-Peter-Müller (1958) 공식, Wilcock (2001) 공식과는 반대로 하상토의 종류가 가는 모래나 실트일 경우 적용 가능한 유사량 공식으로 1년 모의와 10년 모의에서는 다른 공식들과 비교했을 경우 변동의 양상이 크게 다르지 않지만 100년 모의의 경우 대상구간의 50km지점 이후에서 침식, 퇴적이 반복적으로 나타나 단면과 단면사이에 약 1m에서 4m의 최심하상고 변화가 나타났다. Toffaleti (1969) 공식의 경우 100년 모의 시 하류에서 약 73km인 지점에서 유사량 공식들 중 가장 많은 퇴적고(8.04m)를 나타냈지만 평균 하상변동량은 0.02m로 큰 폭으로 변화하지 않고 완만하게 변동하였다.

Fig 3. Bed change simulation using Ackers and White (1973) formula

Fig 4. Bed change simulation using Yang (1979) formula

Fig 5. Bed change simulation using Engelund and Hansen (1967) formula

Fig 6. Bed change simulation using Laursen (1958) formula
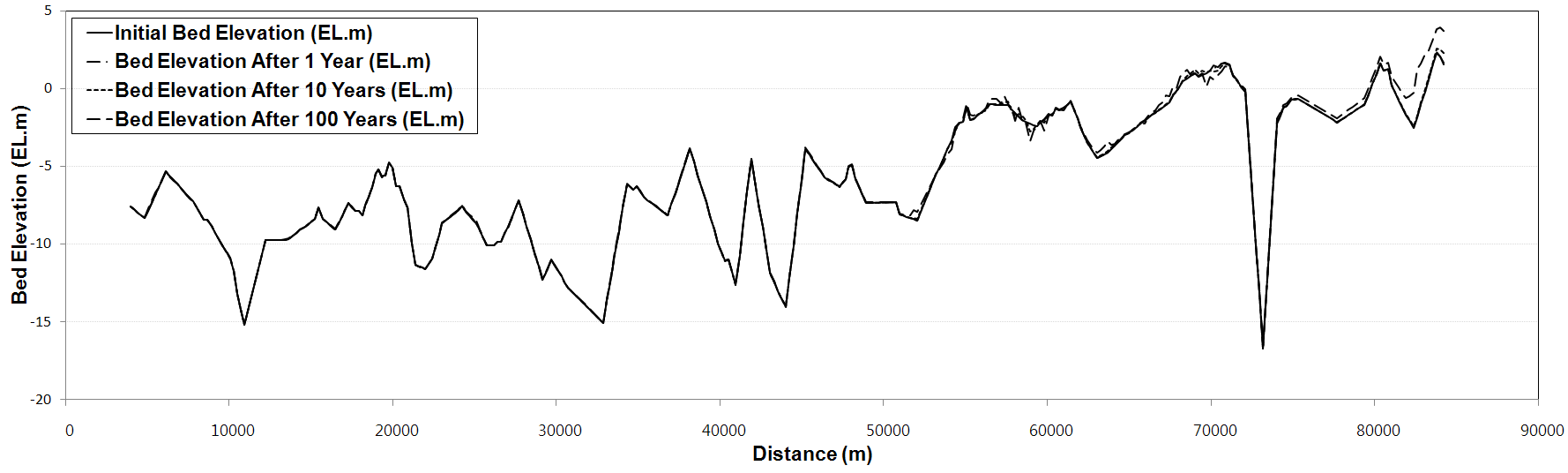
Fig 7. Bed change simulation using Meyer-Peter-Müller (1948) formula

Fig 8. Bed change simulation using Toffaleti (1969) formula

Fig 9. Bed change simulation using Wilcock (2001) formula
Table 2. Maximum sedimentation and Minimum erosion after 1 year

Table 3. Maximum sedimentation and Minimum erosion after 10 years

Table 4. Maximum sedimentation and Minimum erosion after 100 years

5. 결 론
본 연구에서는 HEC-6 모형을 이용하여 낙동강 하류 80km 구간의 유사량 공식별 하상변동 민감도 분석을 수행하였다. 그 결과 1년, 10년, 100년 후의 낙동강 하상변동의 양상과 최대 퇴적, 최대 침식 정도 등을 정량적으로 추정 할 수 있었다. 본 논문에서는 유사량 공식별 하상모의 결과를 종합하여 다음과 같은 결론을 도출하였다.
첫째, 전체적으로 하상변동의 비슷한 양상을 보였던 Engelund and Hansen (1967) 공식, Ackers and White (1973) 공식, Yang (1979) 공식 중 Engelund and Hansen (1967) 공식이 세 공식들 중 가장 큰 하상변동을 모의하는 것으로 분석되었다. 하상변동 값이 가장 크게 분석되었다고 하여 가장 정확하고 최적의 유사량 공식이라고는 설명할 수 없다. 하지만 낙동강 하류의 하상토 및 기타 지형 조건이 비슷한 하천에서는 유사량 실측자료가 전혀 없는 경우 Engelund and Hansen (1967) 공식을 사용함으로써 하천의 퇴적으로부터 야기되는 홍수위 상승, 저수지 기능 감퇴, 용수와 취수 방해, 유사에 의한 오염원 확산 등에 대한 극단적인 현상을 예측하는데 활용할 수 있을 것이다.
둘째, 본 연구에서 Meyer-Peter-Müller (1948) 공식, Wilcock (2001)을 적용한 결과, 하상변동이 최상류에서만 나타날 뿐 하류로 갈수록 변동이 없는 것으로 나타났다. 또한 Laursen (1958) 공식은 모의기간 1년, 10년에서는 다른 공식들과 비슷한 양상의 결과가 나타났으나 모의기간이 100년 일 경우, 모의구간의 상류 일부구간에서 1m에서 4m 폭의 연속적인 하상 고저 현상이 나타났다. Meyer-Peter-Müller (1948) 공식, Wilcock (2001) 공식은 유사의 입자가 큰 소류사 모의 공식이며 Laursen (1958) 공식은 유사 입자가 가는 모래나 실트와 같이 하상토 크기가 매우 작은 경우 적용 가능한 공식이다. 본 연구의 대상하천인 낙동강 하류의 유사 입자크기(중앙입경)는 진동지점 0.3mm, 구포지점 0.25mm으로 일반적인 모래하천의 유사입경 정도의 크기라 할 수 있다. 이와 같은 유사량 공식의 적용 한계성은 하상변동 모의 결과에도 영향을 미치는 것으로 나타났으며 특히 Meyer-Peter-Müller (1948) 공식, Wilcock (2001) 공식을 가는 입자로 구성되어 있는 하천에 적용했을 경우 하상변동이 거의 발생하지 않거나 모의기간이 100년일 경우 실제 하천에서 거의 발생 불가능한 하상형태를 예측하는 것으로 나타났다.
셋째, 낙동강 하류의 하상변동 모의는 하상변동의 실측자료가 있을 경우 이를 활용하여 수치모의에 활용하고자하는 수치모형을 직접적으로 검보정하는 것이 유사량 자료를 유사량 공식들과 비교하여 공식을 선정하는 방법보다 더 개선된 방법이라 할 수 있다. 이를 위해, 다른 유사량 공식들에 비해 하상변동 변화가 서로 비슷한 것으로 나타난 Ackers and White (1973) 공식, Engelund and White (1967) 공식, Yang (1979) 공식, Toffaleti (1969) 공식을 사용하는 것이 적합할 것으로 판단된다.
본 연구에서는 각 유사량 공식에 따라 모의된 하상변동의 차이는 공식별로 매우 크게 나타나고 있으며 하상변동 수치모의시 유사량 공식에 대해 매우 신중하게 검토한 후 선정해야 하는 것으로 나타났다. 본 연구 결과들을 기초로 보다 정확한 하상변동의 예측을 위해서는 실측 된 유사량 자료가 필수적이며 유사량 자료뿐만 아니라 대상하천에 실측 하상변동 자료가 있다면 이와 직접적인 하상변동량의 비교를 통해 대상하천의 적합한 유사량 공식을 선정할 수 있을 것이다.
참 고 문 헌
1. 건설교통부, 1991, 낙동강 하천정비기본계획.
2. 건설교통부, 2001, 서낙동강 하천정비기본계획
3. 건설교통부, 2006, 낙동강수계 본류(구포 등 3개소) 유량측정조사.
4. 고수현, 송인렬, 심창석, 2004, 유사량 산정공식에 따른 유사 및 하상변동 예측에 관한 연구,
5. 한국환경과학회지, Vol 13, No. 3, pp. 263-277.
6. 김진흥, 김상수, 2002, 자연 하천에서 총유사량 측정 및 분석, 한국과학연구, Vol 13, No 1.
7. 남선우, 1978, 하천의 유사량과 하상변동에 관한 연구, 한국수문학회지, 제11권, 제1호.
8. 박정웅, 1984, 홍수시의 하상변동에 관한 연구, 공학박사학위논문, 한양대학교.
9. 서일원, 1994, 하상변동 예측기법의 개발연구. 국제수문개발계획(IHP)연구 보고서.
10. 우효섭, 유권규, 1991, 하상변동 예측모형의 비교분석, 한국건설기술연구원.
11. 지운, Julien. Pierrer Y, 박상길, 김병달, 2008, 낙동강 하류의 유사특성과 낙동강 하구둑 준설효과에 관한 수치모의 연구, 대한토목학회논문집, Vol. 28, No. 4.
12. 한국수자원공사, 2007, 낙동강하구둑 종합관리를 위한 유지관리 개선 연구.
13. 한국수자원공사, 2008, 낙동강 하구둑 유지관리 개선방안 연구 보고서.
14. Ackers, P. and White, W.R.. 1973, Sediment transport: New approach and analysis. J. Hyd. Div. ASCE, 99, no. HY11: pp. 2041-2060.
15. Chang, H.H., Hill, J.C, 1977, Minimum stream power for rivers and deltas, Journal of the Hydraulics Division, ASCE, Vol. 103, No.HY12, pp.1375-1387.
16. Chen, Y.H., Holly F.M., Mahmood, K., Simons, D.B., 1975, Transport of Material by Unsteady Flow, In: Unsteady Flow in Open Channels, Water Resources Publications, Fort Collins, Colorado, Vol. 1, pp.313-365.
17. Engelund, F. and Hansen, E., 1967, A Monograph on Sediment Transport to Alluvial Streams., Copenhagen, Teknik Vorlag.
18. HEC, 1995, HEC-6 Scour and Deposition in River and Reservoirs User`s Manual, US Army Corps of Engineers, Hydrologic Engineering Center.
19. Ji, U., 2006, Numerical model for sediment flushing at the Nakdong River Estuary Barrage, Ph.D. Colorado State University, Fort Collins, Colorado, U.S.A.
20. Laursen, E. M., 1958, The total sediment load of streams, Journal of the Hydraulics Div., ASCE, 84(1).
21. Meyer-Peter, E. and Müller, R., 1948, Fomula for bed-load transport, Proceedings of International Association for Hydraulic Research, 2nd Meeting, Stockholm.
22. Toffaleti, F. B., 1969, Definitive computations of sand discharge in rivers, Journal of the Hydraulics Division, ASCE, 95(HY1).
23. Thomas, W.A, Prasuhn, A.L, 1977, Mathematical modeling of sediment transport scour and deposition in river channels, 17th Congress, IAHR, Vol. 1, pp.137-144.
24. Wilcock, P. R., 2001, Toward a Practical Method for Estimating Sediment-Transport Rates in Gravel Bed Rivers, Earth Surface Processes and Landforms, 26, 1395-1408.
25. Yang, J. C., 1986, Numerical simulation of bed evolution in multi-channel river systems. Ph. D., Thesis Dissertation, The University of Iowa, Iowa City, Iowa.
26. Yang, C. T., 1979, Unit Stream Power Equation for Total Load., J. Hyd. Div. ASCE, vol. 40: pp. 123-138.
27. Yang, C. T., 1998, Simulation and Prediction of River Mophologic Changes Using GSTARS 2.0", International Conference on Hydro-Science and Engineering, Cottbus/Berlin, Germany.
28. Yang, C. T., 2003, SEDIMENT TRANSPORT THEORY AND PRACTICE.
'Tech > 삼안기술지' 카테고리의 다른 글
| [21년01월] 6. 고속도로 인터체인지 연결로 운영속도(V85)조사 및 분석에 관한 연구 (0) | 2021.01.18 |
|---|---|
| [21년01월] 5. 아스팔트를 이용한 마찰증대 매트의 기술개발 (0) | 2021.01.12 |
| [21년01월] 3. 파키스탄 Jhelum 강의 퇴적물 수송 분석 및 준설 계획 (0) | 2021.01.11 |
| [21년01월] 2. 유기물 부하에 따른 Anaerobic digestion 및 Bio-electrochemical anaerobic digestion의 박테리아 군집 (0) | 2021.01.11 |
| [21년01월] 1. 수돗물 깔따구 유충발생 사고의 원인 및 정부 정책방향 (0) | 2021.01.06 |




